El inventor y el rey
- TruthSeeker
- Master Gurú

- Mensajes: 1223
- Registrado: Vie May 16, 2008 10:09 am
El inventor y el rey
Se dice que cuando se inventó el ajedrez, un rey estaba tan agradecido con el inventor que le prometió concederle cualquier deseo. El inventor pidió que en el tablero de ajedrez, en la primera casilla, dejara una grano de trigo, en la segunda dos granos de trigo, en la tercera cuatro, y así sucesivamente (duplicando la cantidad en cada cuadro que se avanzara). Al principio el rey se sorprendió de la facilidad para conceder ese deseo. Trajeron una bolsa de trigo y pusieron manos a la obra. Después de cierto tiempo, al ver que la bolsa de trigo no alcanzaba para satisfacer la promesa, trajeron otra. Después de algún tiempo mas, al ver que después de vaciar sacos y sacos de trigo, y no poder satisfacer la promesa, el rey se desesperó, y mando llamar al matemático de la corte. Los cálculos del matemático mostraron que ni siquiera con la producción de trigo de todo el reino producida durante muchos siglos bastaría para cumplir la promesa.
Este cuento ya está muy trillado, pero de todas formas lo escribo para los que no se lo sabían. ¿Porque no era posible satisfacer la petición del inventor?
(Continúa)
Este cuento ya está muy trillado, pero de todas formas lo escribo para los que no se lo sabían. ¿Porque no era posible satisfacer la petición del inventor?
(Continúa)
- starmans
- Ciudadano Ilustre

- Mensajes: 995
- Registrado: Jue Jun 21, 2007 9:00 pm
- Ubicación: En un bosque inexplorado
- Contactar:
Re: El inventor y el rey
Yo me sabía este cuento pero con frijoles y herraduras de caballo...
No soy ni regular en matemáticas pero el tablero de ajedrez tiene 64 casillas si ponemos un grano de trigo ( o de lo que sea ) en la primera y vamos duplicando el numero conforme avanzamos veremos que solo en la primera fila tendremos 128 granos...
ya en el primer cuadro de la segunda fila tendremos 256 y así sucesivamente.
Como vemos en cada cuadro aumenta el doble y despues de cierto cuadro ya es una cantidad enorme de trigo ( o de frijoles , o lo que sea ) , voy a buscar el cuento de los frijoles para poder explicarlo mejor o si deseas tu TruthSeeker, pon el desglose para verlo mejor.
No soy ni regular en matemáticas pero el tablero de ajedrez tiene 64 casillas si ponemos un grano de trigo ( o de lo que sea ) en la primera y vamos duplicando el numero conforme avanzamos veremos que solo en la primera fila tendremos 128 granos...
ya en el primer cuadro de la segunda fila tendremos 256 y así sucesivamente.
Como vemos en cada cuadro aumenta el doble y despues de cierto cuadro ya es una cantidad enorme de trigo ( o de frijoles , o lo que sea ) , voy a buscar el cuento de los frijoles para poder explicarlo mejor o si deseas tu TruthSeeker, pon el desglose para verlo mejor.
Un creyente se vuelve ateo cuando pierde la fe.
Un ateo se vuelve creyente cuando pierde la razón.
"Las explicaciones místicas pasan por profundas: la verdad es que no son siquiera superficiales." (Nietzsche)
Un ateo se vuelve creyente cuando pierde la razón.
"Las explicaciones místicas pasan por profundas: la verdad es que no son siquiera superficiales." (Nietzsche)
- TruthSeeker
- Master Gurú

- Mensajes: 1223
- Registrado: Vie May 16, 2008 10:09 am
Re: El inventor y el rey
En el primer cuadro tenemos 1 grano de trigo, es decir:
1=2^0 (2 elevado a la 0 potencia)
En el segundo cuadro tenemos:
2=2^1 (2 elevado a la 1 potencia)
En el tercero:
4=2^2 (2 elevado al cuadrado)
En el cuarto:
8=2^3 , etc.
Es decir, ya que el tablero de ajedrez tiene 64 cuadros, en el ultimo cuadro solamente tendríamos:
2^63 granos de trigo = 9,223,372,036,854,775,808 granos de trigo (mas de nueve trillones de granos de trigo)
Para calcular la suma total usamos una formula matemática para las progresiones geométricas:
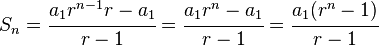
Tomamos a1=1, r=2, n=64
para obtener una suma total de
S=18,446,744,073,709,551,615 (¡mas de 18 trillones de granos de trigo!)
Nada mas queda estimar el peso de un grano de trigo, multiplicarlo por el numero de granos y convertir el resultado a toneladas.
El cuento continua. ¿Alguien tiene interés en saber como salió el rey del problema?
1=2^0 (2 elevado a la 0 potencia)
En el segundo cuadro tenemos:
2=2^1 (2 elevado a la 1 potencia)
En el tercero:
4=2^2 (2 elevado al cuadrado)
En el cuarto:
8=2^3 , etc.
Es decir, ya que el tablero de ajedrez tiene 64 cuadros, en el ultimo cuadro solamente tendríamos:
2^63 granos de trigo = 9,223,372,036,854,775,808 granos de trigo (mas de nueve trillones de granos de trigo)
Para calcular la suma total usamos una formula matemática para las progresiones geométricas:
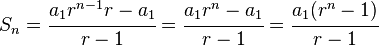
Tomamos a1=1, r=2, n=64
para obtener una suma total de
S=18,446,744,073,709,551,615 (¡mas de 18 trillones de granos de trigo!)
Nada mas queda estimar el peso de un grano de trigo, multiplicarlo por el numero de granos y convertir el resultado a toneladas.
El cuento continua. ¿Alguien tiene interés en saber como salió el rey del problema?
- starmans
- Ciudadano Ilustre

- Mensajes: 995
- Registrado: Jue Jun 21, 2007 9:00 pm
- Ubicación: En un bosque inexplorado
- Contactar:
Re: El inventor y el rey
Yo si tengo interés , porque en el cuento de los frijoles que mencioné , el comerciante ( pues no era un rey ) no pudo salir del atolladero y tuvo que pagarle al protagonista la cantidad de frijoles ( y tampoco era un ajedrez, se trataba de herraduras de caballo ) para no hacer enredos... busco el cuento.
Un creyente se vuelve ateo cuando pierde la fe.
Un ateo se vuelve creyente cuando pierde la razón.
"Las explicaciones místicas pasan por profundas: la verdad es que no son siquiera superficiales." (Nietzsche)
Un ateo se vuelve creyente cuando pierde la razón.
"Las explicaciones místicas pasan por profundas: la verdad es que no son siquiera superficiales." (Nietzsche)
- TruthSeeker
- Master Gurú

- Mensajes: 1223
- Registrado: Vie May 16, 2008 10:09 am
Re: El inventor y el rey
Bueno, entonces continuamos con el cuento.
El rey había estado muy preocupado y no sabía como salir del problema, hasta un día en que se presentó un matemático a la corte del rey ofreciéndole ayuda. El rey aceptó y conversaron con el inventor, para hacerle una nueva propuesta. Le ofrecieron aumentar mas cuadros al tablero de ajedrez y seguir incrementando el número de cuadros, todo lo que el inventor quisiera, incluso indefinidamente. El rey se preocupó aún mas, creyendo que el matemático lo había metido en problemas peores, y el inventor aceptó la propuesta, muy satisfecho al pensar que aumentaría aún mas su riqueza con la nueva propuesta. La suma total sería:
S=1+2+4+8+16+32+... (una suma con un número infinito de términos)
Es decir, el inventor aparentemente recibiría una cantidad infinita de granos de trigo (lo que evidentemente no es posible). Factorizamos el 2 en la suma de arriba a partir del segundo termino:
S=1+2(1+2+4+8+16+...)
Lo que está dentro del paréntesis es igual a la suma misma, por lo que podemos escribir:
S=1+2S
Resolvemos la ecuación:
S-2S=1
-S=1
S=-1
¡La suma total es -1! ¡El inventor le quedó debiendo al rey un grano de trigo! Evidentemente el resultado del calculo no es correcto. Debe haber algún error en el procedimiento. ¿Cual es?
El rey había estado muy preocupado y no sabía como salir del problema, hasta un día en que se presentó un matemático a la corte del rey ofreciéndole ayuda. El rey aceptó y conversaron con el inventor, para hacerle una nueva propuesta. Le ofrecieron aumentar mas cuadros al tablero de ajedrez y seguir incrementando el número de cuadros, todo lo que el inventor quisiera, incluso indefinidamente. El rey se preocupó aún mas, creyendo que el matemático lo había metido en problemas peores, y el inventor aceptó la propuesta, muy satisfecho al pensar que aumentaría aún mas su riqueza con la nueva propuesta. La suma total sería:
S=1+2+4+8+16+32+... (una suma con un número infinito de términos)
Es decir, el inventor aparentemente recibiría una cantidad infinita de granos de trigo (lo que evidentemente no es posible). Factorizamos el 2 en la suma de arriba a partir del segundo termino:
S=1+2(1+2+4+8+16+...)
Lo que está dentro del paréntesis es igual a la suma misma, por lo que podemos escribir:
S=1+2S
Resolvemos la ecuación:
S-2S=1
-S=1
S=-1
¡La suma total es -1! ¡El inventor le quedó debiendo al rey un grano de trigo! Evidentemente el resultado del calculo no es correcto. Debe haber algún error en el procedimiento. ¿Cual es?
- Lalo Marquez
- Super Moderador

- Mensajes: 2700
- Registrado: Mié Feb 26, 2003 10:00 pm
- Posición: Escéptico
- Ubicación: México
- Contactar:
Re: El inventor y el rey
Yo soy pésimo para las matemáticas, de manera que no quiero ni comenzar a quebrarme la cabeza a tratar de responder, pero no podía dejar de comentar que yo no me sabía esta otra parte del cuento, así que me tienes en suspenso por saber cómo termina esta versión mejorada.
- Moravec
- Moderador

- Mensajes: 1083
- Registrado: Lun Mar 03, 2003 10:00 pm
- Ubicación: Rancho del Rey 91910
- Contactar:
Re: El inventor y el rey
Interesante triquiñuela esa del matemático del rey estimado Truthseeker, confieso que yo ignoraba por completo esa segunda parte de la historia 
Me parece que el error consiste en considerar que se puede tener dos veces S. Que sería equivalente a decir "dos veces el infinito" lo cuál es imposible.
Me parece que el error consiste en considerar que se puede tener dos veces S. Que sería equivalente a decir "dos veces el infinito" lo cuál es imposible.
Ipsa scientia potestas est.
Amicus Plato, sed magis amica veritas.
Amicus Plato, sed magis amica veritas.
- TruthSeeker
- Master Gurú

- Mensajes: 1223
- Registrado: Vie May 16, 2008 10:09 am
Re: El inventor y el rey
superflash escribió:Yo soy pésimo para las matemáticas, de manera que no quiero ni comenzar a quebrarme la cabeza a tratar de responder, pero no podía dejar de comentar que yo no me sabía esta otra parte del cuento, así que me tienes en suspenso por saber cómo termina esta versión mejorada.
Sabía que el cuento era muy conocido (a excepción de la segunda parte). La primera parte del cuento se usa para explicar el comportamiento vertiginoso del crecimiento exponencial. La segunda parte puede ser útil para explicar que son las indeterminaciones y las paradojas que surgen cuando tratamos con cantidades infinitas.Moravec escribió:Interesante triquiñuela esa del matemático del rey estimado Truthseeker, confieso que yo ignoraba por completo esa segunda parte de la historia
Me parece que el error consiste en considerar que se puede tener dos veces S. Que sería equivalente a decir "dos veces el infinito" lo cuál es imposible.
El error está en restar S-2S. Aquí tendríamos una indeterminación del tipo:
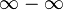
(infinito menos infinito). En cálculo, cuando se enseña límites, se dice que existe una indeterminación, cunado el resultado de un límite puede dar cualquier resultado.
Moravec estaba por el camino correcto.
Todavía estoy esperando la otra versión.starmans escribió:Como vemos en cada cuadro aumenta el doble y despues de cierto cuadro ya es una cantidad enorme de trigo ( o de frijoles , o lo que sea ) , voy a buscar el cuento de los frijoles para poder explicarlo mejor o si deseas tu TruthSeeker, pon el desglose para verlo mejor.
- tequileitor
- Moderador

- Mensajes: 464
- Registrado: Mar Abr 05, 2005 9:00 pm
Re: El inventor y el rey
Mmmm... no creo que vaya por ahí la cosa, recordemos que S=18,446,744,073,709,551,615, (a mi me salió 18,446,744,073,709,600,000) lo cual es un chingo, pero no es igual que infinito. 
Esto se pone bueno...
Saluds.
Esto se pone bueno...
Saluds.
- Moravec
- Moderador

- Mensajes: 1083
- Registrado: Lun Mar 03, 2003 10:00 pm
- Ubicación: Rancho del Rey 91910
- Contactar:
Re: El inventor y el rey
Yo lo veo así estimado Tequileitor:tequileitor escribió:Mmmm... no creo que vaya por ahí la cosa, recordemos que S=18,446,744,073,709,551,615, (a mi me salió 18,446,744,073,709,600,000) lo cual es un chingo, pero no es igual que infinito.
Esto se pone bueno...
Saluds.
El número que calculaste puede ser correcto para la primera propuesta, sin embargo para la segunda propuesta en que le ofrecen al inventor el que aumente el número de cuadros sin límite, entonces S si tiende a infinito.....
Saludos
Moravec
Ipsa scientia potestas est.
Amicus Plato, sed magis amica veritas.
Amicus Plato, sed magis amica veritas.
- starmans
- Ciudadano Ilustre

- Mensajes: 995
- Registrado: Jue Jun 21, 2007 9:00 pm
- Ubicación: En un bosque inexplorado
- Contactar:
Re: El inventor y el rey
Lo que pasa es que no lo he encontrado en internet, yo lo había leído en un "libroalmanaque" de Escuela para Todos del año no me acuerdo cual, entonces voy a buscarlo y lo transcribo, solo pido paciencia.TruthSeeker escribió:Todavía estoy esperando la otra versión.starmans escribió:Como vemos en cada cuadro aumenta el doble y despues de cierto cuadro ya es una cantidad enorme de trigo ( o de frijoles , o lo que sea ) , voy a buscar el cuento de los frijoles para poder explicarlo mejor o si deseas tu TruthSeeker, pon el desglose para verlo mejor.
Un creyente se vuelve ateo cuando pierde la fe.
Un ateo se vuelve creyente cuando pierde la razón.
"Las explicaciones místicas pasan por profundas: la verdad es que no son siquiera superficiales." (Nietzsche)
Un ateo se vuelve creyente cuando pierde la razón.
"Las explicaciones místicas pasan por profundas: la verdad es que no son siquiera superficiales." (Nietzsche)
- TruthSeeker
- Master Gurú

- Mensajes: 1223
- Registrado: Vie May 16, 2008 10:09 am
Re: El inventor y el rey
Esta bueno, tampoco hay demasiado apuro.starmans escribió:Lo que pasa es que no lo he encontrado en internet, yo lo había leído en un "libroalmanaque" de Escuela para Todos del año no me acuerdo cual, entonces voy a buscarlo y lo transcribo, solo pido paciencia.TruthSeeker escribió:Todavía estoy esperando la otra versión.starmans escribió:Como vemos en cada cuadro aumenta el doble y despues de cierto cuadro ya es una cantidad enorme de trigo ( o de frijoles , o lo que sea ) , voy a buscar el cuento de los frijoles para poder explicarlo mejor o si deseas tu TruthSeeker, pon el desglose para verlo mejor.
- tequileitor
- Moderador

- Mensajes: 464
- Registrado: Mar Abr 05, 2005 9:00 pm
Re: El inventor y el rey
[quote="MoravecYo lo veo así estimado Tequileitor:
El número que calculaste puede ser correcto para la primera propuesta, sin embargo para la segunda propuesta en que le ofrecen al inventor el que aumente el número de cuadros sin límite, entonces S si tiende a infinito.....
Saludos
Moravec[/quote]
Perdón, me quedé con la idea de los 64 cuadros del tablero de ajedrez.
Siendo así, me retracto.
Saluds.
El número que calculaste puede ser correcto para la primera propuesta, sin embargo para la segunda propuesta en que le ofrecen al inventor el que aumente el número de cuadros sin límite, entonces S si tiende a infinito.....
Saludos
Moravec[/quote]
Perdón, me quedé con la idea de los 64 cuadros del tablero de ajedrez.
Siendo así, me retracto.
Saluds.